该团队使用贝叶斯方法量化了钽和两种常见爆炸材料的金属强度不确定性,并将其集成到金属/HE 耦合模型中。
劳伦斯利弗莫尔国家实验室 (LLNL) 的一组研究人员首次量化并严格研究了金属强度对准确建模金属/高爆炸物耦合 (HE) 实验的影响,揭示了国家安全和国防应用重要模型中一个难以捉摸的变量。
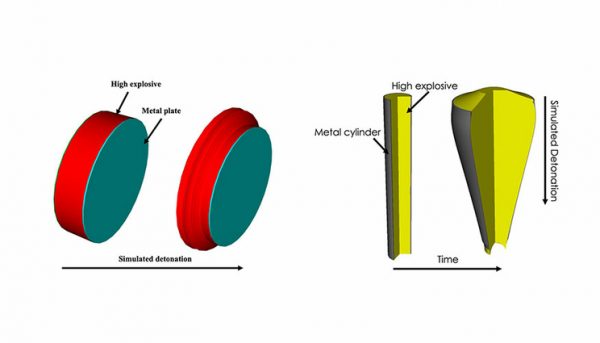
左图是用钽/LX-14 和钽/LX-17 建模的小板测试。右图是用钽/LX-17 建模的圆柱体测试。图片来源:Matt Nelms/LLNL。
该团队使用贝叶斯方法量化了钽和两种常见爆炸材料的金属强度不确定性,并将其集成到金属/HE 耦合模型中。他们的发现可能会为状态方程研究提供更准确的模型,该模型评估材料在不同条件下存在的物质状态。他们的论文(在《应用物理学杂志》(Journal of Applied Physics)上被选为编辑推荐——还表明金属强度的不确定性可能对结果的影响微不足道。
“长期以来,现场传说 HE 模型校准对金属强度很敏感,”该论文的第一作者、LLNL 计算工程部 (CED) 的小组负责人 Matt Nelms 说。“通过使用严格的贝叶斯方法,我们发现情况并非如此,至少在使用钽时是这样。”
在金属/HE 耦合实验中,HE 材料附着在金属上,然后引爆。然后,研究人员测量金属表面的速度,以推断 HE 在从固体转变为气体时的行为。
与许多实验一样,计算机模型帮助高等教育研究人员理解行为并设计测试以获得最佳结果。使模型准确涉及了解不同变量的可能行为范围(称为不确定性),以及所有这些微小的差异如何加起来影响实验结果。对不确定性了解得越多,研究人员就越能更好地将这些知识引入模型,以帮助它做出准确的预测。
金属的强度(其承受力的能力)是最难量化的不确定性,因为爆炸引起的极端条件和动态运动使其难以与 HE 的行为区分开来。该团队使用贝叶斯框架来解决这个问题。贝叶斯分析依靠概率来确定给定效应的可能原因;在本例中为 Predicted Results。
“贝叶斯框架的美妙之处和挑战在于,它对物理学来说很幼稚,”Nelms 说。“这意味着需要非常小心才能确保结果具有物理意义,但也提供了一种偏差较小的工具。”
该团队分析了三种钽金属常见配置的结果:两块板测试,其中 HE(LX-14 或 LX-17)推动一个薄金属盘,以及一个圆柱测试,其中 HE (LX-17) 膨胀一个限制它的金属圆柱体。贝叶斯分析着眼于后验概率,即可能结果的分布,首先纳入了金属强度的不确定性,然后忽略了它。后验之间的差异提供了对金属强度不确定性的良好估计,并显示了它对结果的影响。
Nelms 强调,结果尚不能转移到其他金属上,但方法可以。他希望进一步的研究可以在他们的发现的基础上,既能阐明他们的发现,又能帮助使 HE 模型更加准确,以支持国家安全。
合著者包括 LLNL 的 William Schill、William Kuo、Nathan Barton 和 Kathleen Schmidt。
声明: 此文观点不代表本站立场;转载须要保留原文链接;版权疑问请联系我们。